Question

21. A swimming pool is 60 feet long and 30 feet wide. It is 3 feet deep at one end andslopes evenly to a depth of 9 feet at the other end. How many gallons of water will berequired to fill it to 1 foot from the top? (Hint: (3 + 9) / 2 = 6 ft average depth of pool.)Answer

Answer 1

We have a pool with:

- Length: 60 ft

- Width: 30 ft

- Depth: 3 ft at one end and 9 ft at the other end, with a linear slope.

We have to find how many gallons are needed to fill it to 1 ft from the top.

If we see the pool from the side, we get:

We can see that we can consider the average depth of (3+9)/2 = 6 ft and get the same volume, as the slope is linear.

Then, we can calculate the volume as the product of the length, the width and the actual depth.

The actual depth will be the average depth, 6 ft, minus the depth that is not filled, that is the 1 ft at the top. Then, the actual depth is 5 ft.

Then, the volume is:

`V=L\cdot W\cdot D=60\cdot30\cdot5=9000ft^3`

Now, we have to express this volume in gallons, using the equivalency:

`1ft^3=7.48052gal`
`V=9000ft^3\cdot\frac{7.48052\text{gal}}{1ft^3}=67324.68gal`

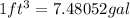
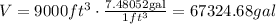
Answer: The volume of water needed is 67,324.68 gallons.