Question

Unpolarized light with intensity 373.85 W/m2 passes first through a polarizing filter with its axis vertical, then through a polarizing filter with its axis 32.57o from vertical. What light intensity emerges from the second filter ?

Answer 1

Given:

The intensity of unpolarized light is: I = 373.85 W/m²

The angle made by the second polarizer filter with the vertical is: θ = 32.57°

To find:

The intensity of the light coming out of the second polarizer filter.

Step-by-step explanation:

When an unpolarized light of intensity I passes through the polarizer, its intensity is reduced by a factor of 1/2.

Thus, the intensity I1 of the polarized light coming out of the first polarizer when an unpolarized light of intensity I passes through it is calculated as:

`I_1=(I)/(2)=\frac{373.85\text{ W/m}^2}{2}=186.925\text{ W/m}^2`

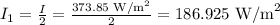
Now, the polarized light of intensity I1 passes through the second polarizer which makes the angle of 32.57° with the vertical.

The intensity I2 of the light coming out of the second polarizer is calculated as:

`I_2=I_1cos^2\theta=186.925\text{ W/m}^2* cos^2(32.57°)=186.925\text{ W/m}^2*0.7102=132.7541\text{ W/m}^2`

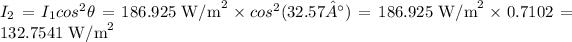
Final answer:

The intensity of light coming out of the second polarizer filter is 132.7541 W/m².