Question

Solve by Completing the Square! x^2+ 6x + 8 = 0

Answer 1

The value of x are -2 and -4

Step-by-step explanation:

Given the equation

`x^2+6x+8=0`

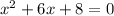
To solve this by completing the square, first of all, we need to rewrite the equation as

`x^2+2(3x)+8=0\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots.(1)`

Note that:

`\begin{gathered} (x+a)^2=x^2+2ax+b^2\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots(2) \\ \\ (x-b)^2=x^2-2ax+b^2\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\text{.}(3) \end{gathered}`

If we write equation (1) as

`x^2+2(3x)+3^2`

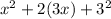
we have:

`(x+3)^2`

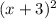
But

`x^2+2(3x)+3^2=x^2+6x+9`

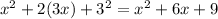
This is equation (1) with an addition of 1.

Subtracting 1 from this will give us exactly equation (1)

`(x+3)^2-1=0`

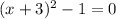
This is exactly equation (1)

Add 1 to both sides of the equation

`(x+3)^2=1`

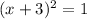
Take square roots of both sides

`\begin{gathered} \sqrt[]{(x+3)^2}=\pm\sqrt[]{1} \\ \\ x+3=\pm1 \\ \\ \text{Subtract 3 from both sides} \\ x=-3\pm1 \end{gathered}`

Therefore,

x = -3 + 1 = -2

OR

x = -3 - 1 = -4