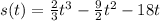
To find when the particle is at rest, equal the velocity function (derivate of the position function) to 0 and solve t:
Velocity function:
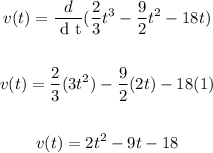
Equal to 0 the equation above:
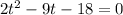
Solve t:
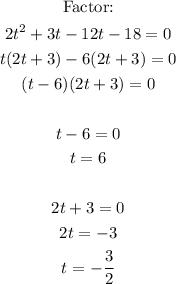
Solutions for t are: t=6 and t=-3/2.
As the time cannot be a negaive amount. The particle is at rest at a time of 6