Question

The lateral area of a pyramid with a square base is 1280 in.² its base edges are 32 inches long. Find the height of the pyramid.

Answer 1

The height, h of the pyramid = 12 inc

Step-by-step explanation

Given:

Lateral area, L.A = 1280 in.²

Base edge, a = 32 inches

What to find:

The height, h of the pyramid.

Step-by-step solution:

The formula for the lateral area of a square based pyramid is given by

`L.A=a\sqrt{a^2+4h\placeholder{⬚}^2}`

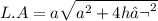
Putting the values of the given parameters into the formula, height h of the pyramid is calculated as follows.

`\begin{gathered} 1280=32\sqrt{32^2+4h\placeholder{⬚}^2} \\ \\ Square\text{ }both\text{ }sides \\ \\ 1280^2=32^2(32^2+4h^2 \\ \\ (1280^2)/(32^2)=32^2+4h^2 \\ \\ 4h^2=(1280^2)/(32^2)-32^2 \\ \\ 4h^2=1600-1024 \\ \\ 4h^2=576 \\ \\ Divide\text{ }both\text{ }sides\text{ }by\text{ }4 \\ \\ (4h^2)/(4)=(576)/(4) \\ \\ h^2=144 \\ \\ h=√(144) \\ \\ h=12\text{ }inches \end{gathered}`