Question

Shawn and Mary wrote down two different functions that have the same rate of change. Shawn's function is represented by the table shown. Graph a function that could be Mary's function on the coordinate plane below.

Answer 1

To answer this question we will use the following formula to compute the rate of change of a linear function:

`(y_1-y_2)/(x_1-x_2).`

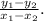
Then the rate of change of Shawn's function is:

`(-5-(-1))/(-1-1).`

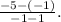
Simplifying the above result we get:

`\begin{gathered} (-5+1)/(-2), \\ (-4)/(-2), \\ 2. \end{gathered}`

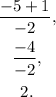
Then, the graph of Mary's function is a line with a slope of 2 that does not passes through (1,-1), for example:

`y=2x.`

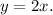
Answer: