The LCM is the smallest number that is a multiple of the given numbers.
To find it we can make a list of the multiples for each number until we find the smallest multiple they have in common, also we can find the prime factorization for each number first:
Prime factorization for 62:
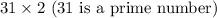
Prime factorization for 36:
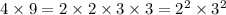
Prime factorization for 24:
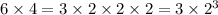
For each prime factor, let's find where it occurs most often as a factor and write it that many times in a new list:
New list: 31, 3, 2: 31 occurs one time, 3 occurs most often two times in the prime factorization for 36, and 2 occurs most often three times in the prime factorization for 24, then the LCM is:

Answer: The LCM of 24, 36 and 62 is 2232