Question

Depreciation is the decrease or loss in value of an item due to age, wear, or market conditions. We usually consider depreciation on expensive items like cars. Businesses use depreciation as a loss when calculating their income and taxes.One company buys a new bulldozer for $141200. The company depreciates the bulldozer linearly over its useful life of 25 years. Its salvage value at the end of 25 years is $16200. A) Express the value of the bulldozer, V, as a function of how many years old it is, t. Make sure to use function notationB) The value of the bulldozer after 13 years is $

Answer 1

a) V=-5000t+141200

b)after 13 years the bulldozer´s value will be 76200

Step-by-step explanation

Step 1

set the equation:

as the bulldozer depreciates linearly, we can use a linear function to represent the situatio.

a linear function has the form

`\begin{gathered} y=\text{ mx+b} \\ where\text{ m is the slope and b is the y-intercept} \end{gathered}`

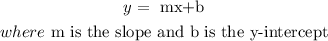
so

a) let t represent s the time

let V represents the value of the bulldozer

so, we have 2 coordinates

I)One company buys a new bulldozer for $141200

`\begin{gathered} value=\text{ 141200} \\ time\text{ = 0} \\ so \\ P1(0,141200) \end{gathered}`

ii) Its salvage value at the end of 25 years is $16200,so

`\begin{gathered} value=\text{ 16200} \\ time=25 \\ so \\ P2(25,16200) \end{gathered}`

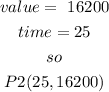
b) now, we have 2 points, we can find the slope using the formula

the slope of line is given by:

`slope=\frac{change\text{ in y }}{chang\text{e in x}}=(\Delta y)/(\Delta x)=(y_2-y_1)/(x_2-x_1)`

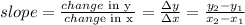
then, let

`\begin{gathered} P1(0,141200) \\ P2(25,16200) \end{gathered}`

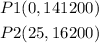
replace to find the slope

`\begin{gathered} slope=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ slope=(16200-141200)/(25-0)=(-125000)/(25)=-5000 \end{gathered}`

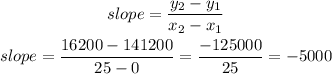
so, the slope of the line is -5000

c) finally,get the function of the line, use the slope-point equation

`\begin{gathered} y-y_1=m(x-x_1) \\ where\text{ m is the slope } \\ (x_1,y_1)\text{ is a well known point} \end{gathered}`

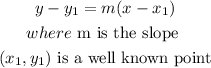
so,let

`\begin{gathered} slope=-5000 \\ P(0,141200) \end{gathered}`

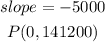
replace and solve for y

`\begin{gathered} y-y_(1)=m(x-x_(1)) \\ y-141200=-5000(x-0) \\ y-141200=-5000x \\ add\text{ 141200in both sides} \\ y-141200+141200=-5,000x+141200 \\ y=-5000x+141200 \end{gathered}`

finally, rewrite the functino using the original variable

`\begin{gathered} y=-5,000x+141,200 \\ V=-5000t+141200\Rightarrow equation \end{gathered}`

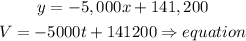
so,

a) V=-5000t+141200

Step 2

now, the value after 13 years,

to know that,let t = 13 and evaluate

`\begin{gathered} \begin{equation*} V=-5000t+141200 \end{equation*} \\ V=-5000(13)+141200 \\ V=-65000+141200 \\ V=76200 \end{gathered}`

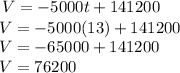
therefor, after 13 years the bulldozer´s value will be 76200

I hope this helps you