It is given that
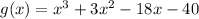
The one factor of g(x) is (x+5).
By using the synthetic method, we get
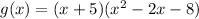
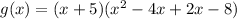
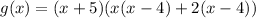
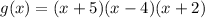
Hecne zeros of g(x) is -5,4, and -2.
2)
It is given that
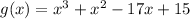
The one zero of the given g(x) is x=1.
By using the synthetic method, we get
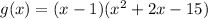
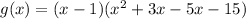
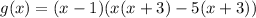
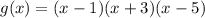
To find zeros of g(x) by equating g(x) to zero.
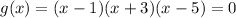
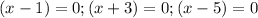
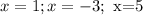
Hence the zeros of the given function g(x) are 1,-3, and 5.