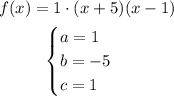First, we need to find the y-intercept. For this, we need to understand that the 'y intercept' refers to the point(s) of the function in which x=0 and y have some value.
So, we set x=0 and obtain:
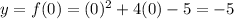
So, the function intercepts the y axis on (0,-5)
As for identifying the zeros of the function, this can be done by asking which are the values of x such that f(x)=0. So, if f(x)=0
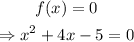
And this is simply a quadratic equation, we can choose whatever method we want to solve it, one way is the next:
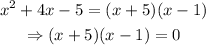
So, the zeros of the function are x=-5 and x=1
Finally, we need to rewrite the formula in intercept form.
This is a quadratic equation, in general, the intercept form of this kind of functions is:
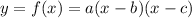
Where a, b, and c are constants.
So, by finding the zeros of the function, we have already found the intercept form: