The trigonometric identity secant is equal to:
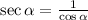
In the unit circle, the cosine is given by the x-coordinate, then, here we have the unit circle:
As we said before, the cosine of an angle is the x-coordinate, then:
![\cos (3\pi)/(4)=\frac{-\sqrt[]{2}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/o32qj6qdap3cb1or3vnkzt02tbgjh4sclt.png)
And, then the secant is:
![\begin{gathered} \sec (3\pi)/(4)=(1)/(\cos (3\pi)/(4)) \\ \sec (3\pi)/(4)=\frac{1}{\frac{-\sqrt[]{2}}{2}} \\ By\text{ applying the properties of fractions:} \\ \sec (3\pi)/(4)=\frac{2}{-\sqrt[]{2}} \\ \sec (3\pi)/(4)=\frac{2}{-\sqrt[]{2}}\cdot\frac{-\sqrt[]{2}}{-\sqrt[]{2}} \\ \sec (3\pi)/(4)=\frac{-2\sqrt[]{2}}{2} \\ \text{Simplify 2/2=1} \\ \sec (3\pi)/(4)=-\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/h0vzuhof2bm94ykot3hafnivndi0ea2i7x.png)
The answer is the last option.