Question

A food truck sells burgers and hot dogs. During lunch, it sold 88 items for a total of $331. If burgers cost $4.50 and hot dogs cost $3.25, how many of each item were sold?a) The food truck sold 30 burgers and 58 hot dogs.b) The food truck sold 29 burgers and 59 hot dogs.c) The food truck sold 36 burgers and 52 hot dogs.d) The food truck sold 33 burgers and 55 hot dogs.

Answer 1

Let the number of burgers be x and the number of hot dogs be y.

The question gives that the total number of items sold is 88. This can be written to be:

`x+y=88\text{ -------------(1)}`

The cost of a burger is $4.50 while that of hot dogs is $3.25. If the total sold price is $331, we can express this as:

`4.50x+3.25y=331\text{ -----------------(2)}`

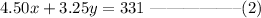
This gives us a pair of equations we can solve simultaneously:

`\begin{gathered} x+y=88\text{ -------------(1)} \\ 4.50x+3.25y=331\text{ -----------------(2)} \end{gathered}`

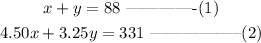
To solve by substitution, make x the subject of the formula in equation (1):

`x=88-y\text{ ----------(3)}`

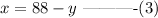
Substitute the value of x into the second equation:

`\begin{gathered} 4.50(88-y)+3.25y=331 \\ 396-4.50y+3.25y=331 \\ -1.25y=331-396 \\ -1.25y=-65 \\ \therefore \\ y=(-65)/(-1.25) \\ y=52 \end{gathered}`

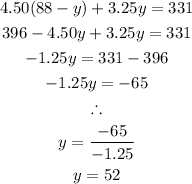
To find x, we can substitute the value of y into equation (3):

`\begin{gathered} x=88-52 \\ x=36 \end{gathered}`

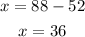
ANSWER:

The correct option is OPTION C: The food truck sold 36 burgers and 52 hot dogs.