We have to find the 99th term of the arithmetic sequence: 2,-3, -8...
First, we have to find the explicit function for this arithmetic sequence.
This mean that we have to find the common difference for this sequence:
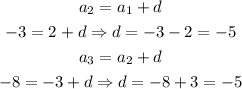
The common difference is d = -5.
We now can find the expression for the explicit function for this sequence as:
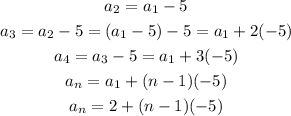
Then, we can find the 99th term by calculating this formula for n = 99:
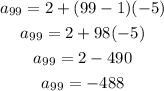
Answer: the 99th of this sequence is -488.