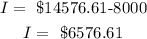To find the value of the compound amount and compound interest:
where A rep Amount
I rep compound interest
(1.a) $4,000 for 7 years at 6% compounded annually.
First, convert R as a percent to r as a decimal
r = R/100
r = 6/100
r = 0.06 rate per year,
Then solve the equation for A
A = P(1 + r/n)nt
A = 4,000.00(1 + 0.06/1)(1)(7)
A = 4,000.00(1 + 0.06)(7)
A = $6,014.52
(b) I = A - P
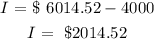
(2a) $5,000 for 20 years at 5% compounded annually.
First, convert R as a percent to r as a decimal
r = R/100
r = 5/100
r = 0.05 rate per year,
Then solve the equation for A
A = P(1 + r/n)nt
A = 5,000.00(1 + 0.05/1)(1)(20)
A = 5,000.00(1 + 0.05)(20)
A = $13,266.49
(b) I = A -P
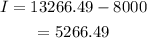
(6a) $8,000 for 3 years at 6¼% compounded daily.
First, convert R as a percent to r as a decimal
r = R/100
r = 3/100
r = 0.03 rate per year,
Then solve the equation for A
A = P(1 + r/n)nt
A = 8,000.00(1 + 0.03/365)(365)(20)
A = 8,000.00(1 + 8.2192E-5)(7300)
A = $14,576.61
(b) I = A - P