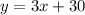For two lines to be parallel, then their slopes are equal in value.
The equation given;
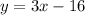
Has its slope given as 3.
The slope of the line when given the equation is the coefficient of x.
Next step, we have a second line passing through the point (-10,0), and its slope is 3 (parallel to the first one given).
We have the following variables as;

The equation is slope-intercept form is;

We can now substitute the values of, x, y and m and we would have;
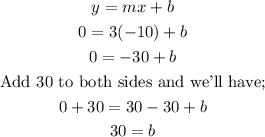
The value of b (the y-intercept) is 30.
The equation can now be properly written as;
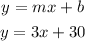
ANSWER: