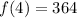
Step-by-step explanation
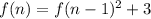
In a recursive formula, each term is defined as a function of its preceding term(s). A recursive formula designates the starting term, a1, and the nth term of the sequence, an
so, we can find the first 4 terms
Step 1
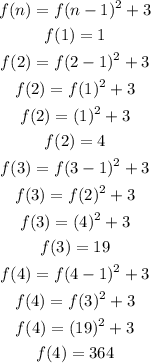
hence, the answer is
I hope this helps you