Question

Suppose 28 blackberry plants started growing in a yard. Absent constraint, the blackberry plants will spread by 85% a month. If the yard can only sustain 90 plants, use a logistic growth model to estimate the number of plants after 5 months.

Answer 1

we have an exponential growth function

`\begin{gathered} y=a(1+r)^x \\ y\leq90 \\ a(1+r)^x\leq90 \end{gathered}`

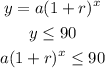
where

a=28

r=85%=85/100=0.85

substitute

`\begin{gathered} 28(1+0.85)^x\leq90 \\ 28(1.85)^x\leqslant90 \end{gathered}`

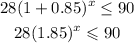
For x=5 months

Find out the value of y and compare it with 90

`\begin{gathered} y=28(1.85)^5 \\ y=607 \end{gathered}`

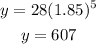
607 > 90

Find out the value of x For y=90

`\begin{gathered} 90=28(1.85)^x \\ (90)/(28)=(1.85)^x \end{gathered}`

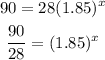
Apply log on both sides

`log((90)/(28))=x*log(1.85)^`

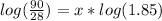
x=1.9 months

therefore

Approximately every 2 months the plants will have to be moved to another site, leaving the initial quantity of 28 plants.

After 5 months the number of plants is about 607