Question

Give the equation of the line passing through the points (-4, 14) and(3,-3).Pls see picture

Answer 1

We need to determine the equation for the line that passes through the two points:

`\begin{gathered} (-4,14) \\ (3,-(7)/(2)) \end{gathered}`

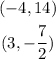
For that we need to determine the slope for the line, which is given by:

`m=(y_2-y_1)/(x_2-x_1)`

Where m is the slope, (x1, y1) and (x2, y2) are the coordinates of the two points.

`\begin{gathered} m=(14-(-(7)/(2)))/(-4-3) \\ m=(14+(7)/(2))/(-7) \\ m=((35)/(2))/(-7) \\ m=-(35)/(14) \end{gathered}`

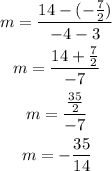
Now we need to use one of the points to determine the full equation, as shown below:

`y-y_1=m\cdot(x-x_1)`

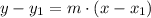
Where (x1, y1) are the coordinates of one of the points.

`y-14=(-35)/(14)(x+4)`

Now we need to isolate the y-variable on the left side.

`\begin{gathered} y=(-35)/(14)x-(35)/(14)\cdot4+14 \\ y=(-35)/(14)x+4 \end{gathered}`

The equation for the line is y = -35x/14 + 4