Answer:
The 95% confidence interval is 157.28 to 167.72
Step-by-step explanation:
Number of coffee, N = 28
Mean, µ = 162.5
Standard deviation, σ = 14.1
Confidence Level, CL = 95%
z-value for 95% confidence interval = 1.96
The confidence interval is calculated below
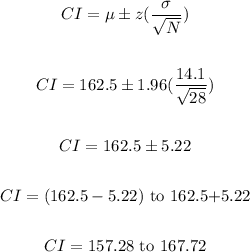
Therefore, the 95% confidence interval is 157.28 to 167.72