Question

You want to invest $5000 compounded monthly. What interest rate will you need to invest it at in order to have $25000 in 10 years?

Answer 1

From the question, we are given that

`\begin{gathered} principal=\text{ \$}5000 \\ Amount=\text{ \$25000} \\ time=10\text{ years} \\ n=12 \end{gathered}`

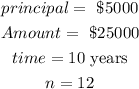
We can then find the rate using the formula below.

`\begin{gathered} r=n\left[\left((A)/(P)\right)^{(1)/(nT)}-1\right] \\ r=12×\left[\left((25000)/(5000)\right)^{(1)/(12*10)}-1\right] \\ r=0.1620276 \end{gathered}`

Therefore, we will convert to percentage.

`\begin{gathered} R=r*100 \\ R=0.1620276*100 \\ R=16.203 \end{gathered}`

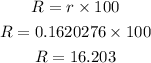
The interest rate required to get a total amount of $25,000.00 from compound interest on a principal of $5,000.00 compounded 12 times per year over 10 years is

Answer: 16.203%