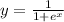
To get a table with values, we have to choose a value for x and calculate the corresponding value for y. For example, choosing x = -5, -2.5, 0, 2.5 and 5.
• x = -5
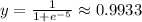
• x = -2.5
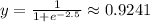
• x = 0
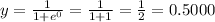
• x = 2.5
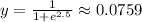
• x = 5
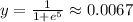
As we can see, higher values of x get near 0, and lower values of x get near 1. As the logistic functions have the form:
Then we can suppose that those values are the asymptotes. To confirm we have to get the limits when x approximates -∞ and +∞:
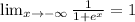
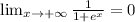
Then our asymptotes are y = 0, 1 and we have no horizontal asymptotes.
Finally, as the x values include from -∞ to +∞, then the domain are all the real values while the range are the values between 0 and 1.
Answer:
• Table
• Asymptotes: ,y = 0, 1 ,and ,x = N/A
,
• Domain: ,all real numbers.
,
• Range: ,(0, 1)
,
• Graph