ANSWER
![undefined]()
Step-by-step explanation
To find the average rate of change of the function, we have to apply the formula:
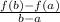
for a ≤ x ≤ b
This implies that:
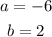
Therefore, the average rate of change of the function is:

To find f(2), we have to substitute 2 for x in the given function:
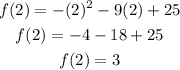
To find f(-6), substitute -6 for x in the given function:
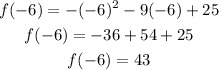
Therefore, the average rate of change of the function is:
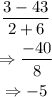
That is the answer.