Two parallel lines have the same slope.
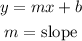
In the given equation the slope is:
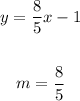
Then, you need to write the equations to slope-intercept form (solve for y) to identiy the slope:
Option 1
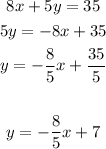
The slope in this one is -8/5. (Is not parallel to the given equation)
Option 2:
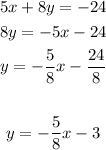
The slope in this one is -5/8. (Is not parallel to the given equation)
Option 3:
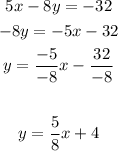
The slope in this one is 5/8. (Is not parallel to the given equation)
Option 4:
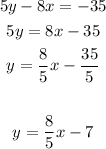
The slope in this one is 8/5. This line is parallel to the given equation.
Answer: Option 4 (5y-8x=-35)