Question

Expand the following binomial using Pascal’s Triangle. Include writing out Pascals’s Triangle to as many rows as necessary to solve this problem. (5x-2y)^4

Answer 1

Given:

`(5x-2y)^4`

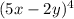
Below is a Pascal's Triangle.

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

Since the exponent we have is 4, counting from zero , we need the last row to expand.

Since the second term in the parenthesis is negative, we shall alternate the sign.

We can now begin the expansion;

(5x - 2y)⁴ = (5x)⁴(2y)⁰ - (5x)³(2y)¹ + (5x)²(2y)² - (5x)¹(2y)³ + (5x)⁰ (2y)⁴

= 625x⁴(1) - 125x³(2y) + 25x² (4y²) - 5x(8y³) + 1(16y⁴)

= 625x⁴ - 250x³y + 100x²y² - 40xy³ + 16y⁴