Question

Match each missing side length and angle with the correct value. Angle measurements are rounded to the nearest hundredth. 15 M LIE, 10 8 8 N 20 22 36.87 32.23° 12 28.07 53.13 17 6 LY MZNMY NM MZNLY Ehts reserved

Answer 1

Now, let us split the triangle in the picture into two as shown below

Now from the diagram above, we can see the two right-angle triangles.

From the smaller triangle NLY, to find the side LY, we will use the Pythagorean theorem. From the Pythagorean theorem

`\text{hypotenuse}^2=opposite^2+adjacent^2`

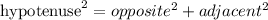
From here we have that

`\begin{gathered} |NL|^2=|NY|^2+|LY|^2 \\ 10^2=8^2+|LY|^2 \\ 100=64+|LY|^2 \\ |LY|^2=100-64 \\ |LY|^2=36 \\ \text{square root both sides } \\ \sqrt[]^2=\sqrt[]{36} \\ \text{square cancels square root, then } \\ |LY|=\sqrt[]{36} \\ |LY|=6 \end{gathered}`

hence LY is 6

Also form the second triangle NMY, using Pythagoras theorem to find NM, we have that

`\begin{gathered} |NM|^2=|NY|^2+|MY|^2 \\ |NM|^2=8^2+15^2 \\ |NM|^2=64+225 \\ |NM|^2=289 \\ \sqrt[]^2=\sqrt[]{289} \\ |NM|=\sqrt[]{289} \\ |NM|=17 \end{gathered}`

Hence, NM = 17

We will use the trig ratio SOHCAHTOA to find angle NMY. NMY is the marked angle in the second triangle. So so using the sides 8 (opposite) and 15(adjacent) we have

`\begin{gathered} \tan |NMY|=\frac{opposite}{\text{adjacent}} \\ \tan |NMY|=\frac{8}{\text{1}5} \\ \text{when tan moves to the other side it becomes tan}^(-1) \\ |NMY|=\text{tan}^(-1)\frac{8}{\text{1}5} \\ |NMY|=28.07^o \end{gathered}`

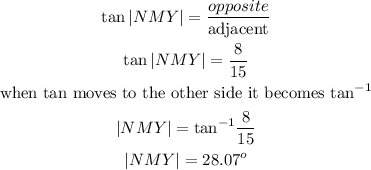
Hence angle NMY = 28.07 degrees

In the first triangle to find angle NLY, using the hypotenuse 10 and the opposite 8, we have

`\begin{gathered} \sin |\text{NLY}|=\frac{opposite\text{ }}{\text{hypotenuse}} \\ \sin |\text{NLY}|=\frac{8}{\text{1}0} \\ |\text{NLY}|=\sin ^(-1)\frac{8}{\text{1}0} \\ |\text{NLY}|=53.13^o \end{gathered}`

Hence angle NLY = 53.13 degrees