Question

Use the sum and difference identities to determine the exact value of the following expression.211sinЗл+43

Answer 1

We are given the following expression:

`\sin ((3\pi)/(4)+(2\pi)/(3))`

the identity for the sum of angles for sines is the following:

`\sin (\alpha+\beta)=\sin \alpha\cos \beta+\cos \alpha\sin \beta`

In this case, we have:

`\begin{gathered} \alpha=(3\pi)/(4) \\ \\ \beta=(2\pi)/(3) \end{gathered}`

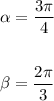
Substituting in the identity we get:

`\sin ((3\pi)/(4)+(2\pi)/(3))=\sin ((3\pi)/(4))\cos ((2\pi)/(3))+\cos ((3\pi)/(4))\sin ((2\pi)/(3))`

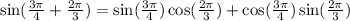
we have the following value:

`\sin ((3\pi)/(4))=\frac{1}{\sqrt[]{2}}`
`\cos ((3\pi)/(4))=-\frac{1}{\sqrt[]{2}}`
`\sin ((2\pi)/(3))=\frac{\sqrt[]{3}}{2}`
`\cos ((2\pi)/(3))=-(1)/(2)`

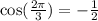
Now, we substitute the values in the indentity:

`\sin ((3\pi)/(4))\cos ((2\pi)/(3))+\cos ((3\pi)/(4))\sin ((2\pi)/(3))=(\frac{1}{\sqrt[]{2}})(-(1)/(2))+(-\frac{1}{\sqrt[]{2}})(\frac{\sqrt[]{3}}{2})`

Simplifying we get:

`(\frac{1}{\sqrt[]{2}})(-(1)/(2))+(-\frac{1}{\sqrt[]{2}})(\frac{\sqrt[]{3}}{2})=-\frac{1}{2\sqrt[]{2}}-\frac{\sqrt[]{3}}{2\sqrt[]{2}}`

Solving the operations:

`-\frac{1}{2\sqrt[]{2}}-\frac{\sqrt[]{3}}{2\sqrt[]{2}}=-0.97`

Therefore, the value of the sine is -0.97