Answer:
3. y ≤ 10
Explanation:
Given the function:
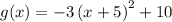
We want to find the range.
The range of a function is the set of all the values of y for which a function is defined.
Compare g(x) with the vertex form of a quadratic function given below:

• The vertex of g(x) = (-5, 10)
Since the value of a is -3 (negative), the parabola opens down and thus, the vertex is a maximum.
• The y-value at the vertex = 10
Thus, the range of g(x) is:
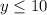
Option 3 is correct.