Question

Both car A and car B leave school when a stopwatch reads zero. Car A travels at a constant 75 km/h, and car B travels at a constant 85 km/h. Draw a position-time graph showing the motion of both cars. How far are the two cars from school when the stopwatch reads 2.0 h? Calculate the distances and show them on your graph.

Answer 1

Distance the cars traveled when t = 2h:

• Car A: 150 km

,

• Car B: 170 km

Graph:

Step-by-step explanation

If both cars travel at a constant speed, it means that the relation between time and distance is constant for each car:

`v=(x)/(t)`

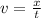
In a position-time graph, the speed v of an object is the slope of the line. So we can rewrite the equation above as:

`x=v\cdot t`

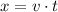
For each car, the distance traveled is:

`\begin{gathered} x_A=75t \\ x_B=85t \end{gathered}`

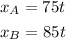
To draw this graph in the provided grid, we have to draw the axis first. The vertical axis is the distance x in kilometers and the horizontal axis is the time in hours.

Next we have to divide each axis with the scale we want and finally draw the lines.

We know that both start at t = 0 and x = 0 - because both cars start in the same spot and at the same time. Then we can find the position at t =2h:

So with this two points we can graph the lines: