The mean of a data set is given by the expression
![\operatorname{mean}=\sum ^N_(n\mathop=0)((1)/(N))a_n]()
Where N is the number of elements of the data set and a_n the different elements in the data set.
Since some elements are repeated we can reduce the former formula into the next expression:
![\operatorname{mean}=\sum ^M_(m=0)((1)/(N))(k_m)a_m]()
Where N is the number of elements in the data set, M is the number of not repeated elements.
Therefore, in the case of our problem:
![\operatorname{mean}=((1)/(N))(9\cdot11+8\cdot5+7\cdot10+11\cdot3)]()
We need to identify N and we can do it by adding up the frequencies:
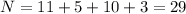
Then, the mean is:
![\operatorname{mean}=(1)/(29)(242)\approx8.345]()