ANSWER
A. True
Step-by-step explanation
Let the complex number be z = a+ ib, so its complex conjugate is z* = a - ib, where a and b are real numbers. Let's find the product,
The product is,
![(a+ib)(a-ib)=a\cdot a-a\operatorname{\cdot}ib+ib\operatorname{\cdot}a-ib\operatorname{\cdot}ib]()
Solve the products,
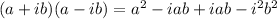
Simplify: note that the second and third terms are opposites, so they cancel out. Remember that i² is equal to -1,
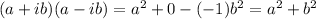
Since a and b were real numbers, then the sum of their squares is also a real number.
Hence, this statement is true.