Given:
The length of yarn needed, l=23 1/4 feet.
The length of a yarn bundle, L=11 1/2 feet.
The number of bundles of yarn needed can be calculated as,
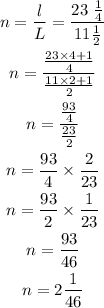
Therefore, 3 bundles is needed by Jenna to make the scarf.
The part of leftover yarn is,
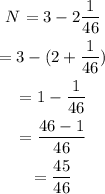
Hence, 45/46 part of a bundle of yarn will be left.
Now, the length of leftover yarn is,
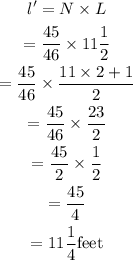
Therefore, 111/4 feet of yarn will be left.