Question

A rectangular loop of wire with a cross-sectional area of 2.936 m2 carries a current of 6.488 A. The loop is free to rotate about an axis that is perpendicular to a uniform magnetic field strength of 1.108 T. The plane of the loop is initially at an angle of 59.914o to the direction of the magnetic field. What is the magnitude of the torque on the loop ?

Answer 1

10.58 Nm

Explanation:

Given:

Area (A) = 2.936 m²

Current (i) = 6.488 A

Magnetic field (B) = 1.108 T

Angle (θ)= 59.914°

To calculate the torque we must resort to the following formula:

`\begin{gathered} \tau=MB\sin\alpha \\ \\ \alpha=90\degree-\theta=90-59.914\degree \\ \\ \alpha=30.086\degree \end{gathered}`

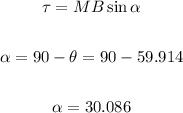
We need to know the magnetic moment, as follows:

`\begin{gathered} M=NIA \\ \\ M=1\cdot6.488\cdot2.936 \\ \\ M=19.05\text{ A}\cdot m^2 \end{gathered}`

In this way we can calculate the torque:

`\begin{gathered} \tau=19.05\cdot1.108\cdot\sin(30.086\degree) \\ \\ \tau=10.58\text{ Nm} \end{gathered}`

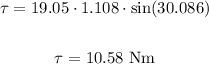
Therefore, the magnitude of the torque on the loop is 10.58 Nm