a)The smaller break even quantity is 10
b)The quantity that must be sold to maximize the profit= 14.25
c)The maximum profit = $36.13
STEP - BY - STEP EXPLANATION
What to find?
• The smaller break even quantity is
,
• The quantity that must be sold to maximize the profit
,
• The maximum profit.
Given:
C(x)= 13x + 370
R(x)=70x - 2x²
a) At the break even quantity, the revenue = cost, that is no profit and no loss.
R(x) = C(x)
So that we have;
70x - 2x² = 13x + 370
Re-arrange.
-2x² + 70x - 13x - 370 =0
-2x² +57x - 370 =0
2x² - 57x + 370 = 0
We can now solve the quadratic equation above.
Using the qudaratic formula
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
a=2 b=-57 c=370
Substitute the values into the formula and evaluate.
![x=\frac{-(-57)\pm\sqrt[]{(-57)^2-4(2)(370)}}{2(2)}](https://img.qammunity.org/2023/formulas/mathematics/college/8mcey3dw2r3y9emlirl3k2yb063cmaxbp9.png)
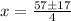
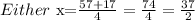
Or

x = 37/2 or x=10
We take the smaller value.
Hence, x=10
Therefore, the smaller break even quantity is 10.
b)To find the quantity that will maximize the profit, find the profit function.
p(x) = R(x) - C(x)
P(x) = 70x - 2x² - (13x +370)
= 70x - 2x² - 13x - 370
P(x) =-2x² + 57x - 370
Equate to zero
-2x² + 57x - 370 = 0
2x² - 57x + 370 =0
The maximum is at x = -b/2a
b= -57 and a=2
Substitute the values
x= - (-57) /2(2)
x= 57 /4
x= 14.25
c) To find the maximum profit, simply substitute x=14.25 into the profit function and simplify.
That is;
P(x) =-2x² + 57x - 370
P(14.25) =-2(14.25)² + 57(14.25) - 370
= -406.125 + 812.25 - 370
= 36.125
≈ 36.13
Hence, the maximum profit is $36.13