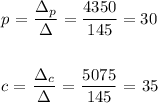Question

Blank 1 - 2850342043504625 Blank 2. - 20253035Blank 3 4350462550755225 Blank 4 20253035

Answer 1

The determinant of the matrix for the pineapple cake is 4350

The price of a pineapple cake is $30

The determinant of the matrix for the chocolate cake is 5075

The price of a chocolate cake is $35

Basically, what we want to do in this question is to form a set of linear equations then use matrix determinant method to solve for the unknowns in the linear equation.

Before we set up these equations,we need to use variables to represent the fruit prices;

Let p represent the price a of pineapple

Let c represent the price of a chocolate;

So let us proceed to form the linear equations;

The equation for the weekdays sales will be;

`45p\text{ + 62c = 3520}`

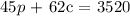
The equation for the weekend sales will be;

`55p\text{ + 79c = }4415`

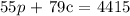
Now, we have two equations that we need to use the matrix determinant method to solve;

`\begin{bmatrix}{45} & {62} \\ {55} & {79} \\ {} & {}\end{bmatrix}\text{ }\begin{bmatrix}{p} & \\ {c} & {} \\ {} & \end{bmatrix}\text{ = }\begin{bmatrix}{3520} & {} & \\ {4415} & {} & \\ {} & {} & \end{bmatrix}`

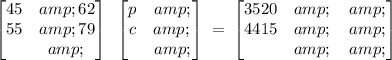
The above is the matrix set up we wil use;

Now, we start by calculating the determinant of 2 * 2 matrix; that would be;

`\begin{gathered} \Delta\text{ = (45 }*\text{ 79) - (62 }*\text{ 55)} \\ \Delta\text{ = 3555-3410 = 145} \end{gathered}`

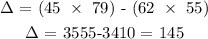
Next is to find the determinant of the pineapple cake matrix;

To find this, what we will do is to substitute the coefficient of p with the total sales value to get a new matrix set;

The matrix for the pineapple cake will be;

`\begin{gathered} \begin{bmatrix}{3520} & {62} \\ {4415} & {79} \\ {} & {}\end{bmatrix}\text{ } \\ \\ \text{The }\det er\min ant\text{ here will be ;} \\ \Delta_{p\text{ = }}(3520\text{ }*\text{ 79) - (62 }*\text{ 4415)} \\ =\text{ 4350} \end{gathered}`

Next is to find the determinant of the chocolate cake matrix;

To find this, what we will do is to substitute the coefficient of c with the total sales value to get a new matrix set;

The matrix for the chocolate cake will be;

`\begin{gathered} \begin{bmatrix}{45} & {3520} \\ {55} & {4415} \\ {} & {}\end{bmatrix} \\ \\ \Delta_c\text{ = (45 }*\text{ 4415) - (55 }*\text{ 3520)} \\ =\text{ 5075} \end{gathered}`

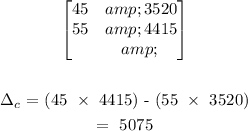
Finally, we proceed to get the prices for the pineapple and the cake;

To get this, we simply divide the matrix of each by the initial matrix value;

`\begin{gathered} p\text{ = }(\Delta_p)/(\Delta)=(4350)/(145)=30_{} \\ \\ c\text{ = }(\Delta_c)/(\Delta)\text{ = }(5075)/(145)\text{ = 35} \end{gathered}`