Question

The 20 kg at angle of 53⁰ in an inclined plane is realsed from rest the coefficient of friction bn the block and the inclined plane are ųs=0.3 and ųk=0.2

A) would the block move
B) if it moves what is its speed after it has descended a distance of 5m down the plane​

Answer 1

Given :-

• A 20kg block at an angle 53⁰ in an inclined plane is released from rest .
• 
  `\mu_s = 0.3 \ \& \ \mu_k = 0.2`

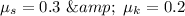
To Find :-

• Would the block move ?
• If it moves what is its speed after it has descended a distance of 5m down the plane .

Solution :-

For figure refer to attachment .

So the block will move if the angle of the inclined plane is greater than the angle of repose . We can find it as ,

`\longrightarrow \theta_(repose)= tan^(-1)(\mu_s)`

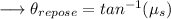
Substitute ,

`\longrightarrow \theta_(repose)= tan^(-1)( 0.2)`

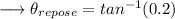
Solve ,

`\longrightarrow\underline{\underline{\theta_(repose)= 16.6^o }}`

Hence ,

`\longrightarrow\theta_(plane)>\theta_(repose)`

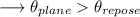
Hence the block will slide down .

Now assuming that block is released from the reset , it's initial velocity will be 0m/s .

And the net force will be ,

`\longrightarrow F_n = mgsin53^o - \mu_k N`

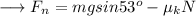
Substitute, N = mgcos53⁰ ( see attachment)

`\longrightarrow ma_n = mgsin53^o - \mu_k mgcos53^o`

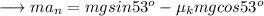
Take m as common,

`\longrightarrow\cancel{m }(a_n) = \cancel{m}( gsin53^o - \mu gcos53^o)`

Simplify ,

`\longrightarrow a_n = gsin53^o - \mu_k g cos53^o`

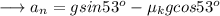
Substitute the values of sin , cos and g ,

`\longrightarrow a_n = 10( 0.79 - 0.2 (0.6))`

Simplify ,

`\longrightarrow a_n = 10 ( 0.79 - 0.12 ) \\\\ \longrightarrow a_n = 10 (0.67)\\\\ \longrightarrow \underline{\underline{a_n = 6.7 m/s^2}}`

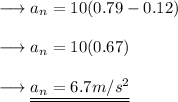
Now using the Third equation of motion namely,

`\longrightarrow2as = v^2-u^2`

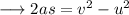
Substituting the respective values,

`\longrightarrow2(6.7)(5) = v^2-(0)^2`

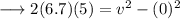
Simplify and solve for v ,

`\longrightarrow v^2 = 67 m/s\\\\\longrightarrow v =√(67) m/s \\\\\longrightarrow\underline{\underline{ v = 8.18 m/s }}`

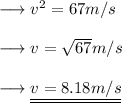
Hence the velocity after covering 5m is 8.18 m/s .