Question

Chords AB and CD intersect as shown nelow find the length of CD

Answer 1

We are asked to determine the length of CD, to do that we will use the following relationship:

`\begin{gathered} CD=21+x+1 \\ CD=22+x \end{gathered}`

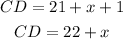
Therefore, we need to determine the value of "x". To do that we will use the intersecting chords theorem, that is:

`(21)(x+1)=(9)(3x-9)`

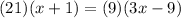
Now we solve for "x" first by applying the distributive law:

`21x+21=27x-81`

Now we will subtract 21 to both sides:

`\begin{gathered} 21x=27x-81-21 \\ 21x=27x-102 \end{gathered}`

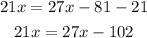
Now we will subtract 27x to both sides:

`\begin{gathered} 21x-27x=-102 \\ -6x=-102 \end{gathered}`

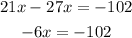
Dividing both sides by -6:

`x=-(102)/(-6)=17`

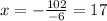
Now we replace the value of "x" in the expression for segment CD:

`\begin{gathered} CD=22+17 \\ CD=39 \end{gathered}`

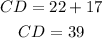
Therefore, the length of CD is 39.