Question

A committee of 6 is to be chosen from the 28 students in a class. If there are 10 males and 18 females in the class, in how many ways can this be done if there must be at least three females on the committee? A: 339864B: 816720C: 3060D: 18564

Answer 1

Hello! First, let's write some important information contained in the exercise:

committee = 6 students

class: 28 students:

- 10 males

- 18 females

Let's consider the rule: At least three females must be on the committee, so we have some cases, look:

_F_ * _F_ * _F_ * __ * __ * __

1st option:

3 females and 3 males

_F_ * _F_ * _F_ * _M_ * _M_ * _M_

2nd option:

4 females and 2 males

_F_ * _F_ * _F_ * _F_ * _M_ * _M_

3rd option:

5 females and 1 male

_F_ * _F_ * _F_ * _F_ * _F_ * _M_

4th option:

6 females and 0 male

_F_ * _F_ * _F_ * _F_ * _F_ * _F_

Now, we have to use the formula below and find the number of possible combinations:

`C_(n,p)=(n!)/(p!\cdot(n-p)!)`

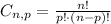
Let's calculate each option below:

1st:

3 females:

`C_(18,3)=(18!)/(3!\cdot(18-3)!)=(18\cdot17\cdot16\cdot15!)/(3\cdot2\cdot1\cdot15!)=(4896)/(6)=816`

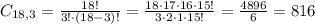
3 males:

`C_(10,3)=(10!)/(3!\cdot(10-3)!)=(10\cdot9\cdot8\cdot7!)/(3\cdot2\cdot1\cdot7!)=(720)/(6)=120`

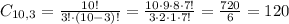
3 females and 3 males: 816 * 120 = 97920

2nd option:

4 females:

`C_(18,4)=(18!)/(4!\cdot(18-4)!)=(18\cdot17\cdot16\cdot15\cdot14!)/(4\cdot3\cdot2\cdot1\cdot14!)=(73440)/(24)=3060`

2 males:

`C2=(10!)/(2!\cdot(10-2)!)=(10\cdot9\cdot8!)/(2\cdot1\cdot8!)=(90)/(2)=45`

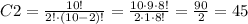
4 females and 2 males: 3060* 45 = 137700

3rd option:

5 females:

`C_(18,5)=(18!)/(5!\cdot(18-5)!)=(18\cdot17\cdot16\cdot15\cdot14\cdot13!)/(5\cdot4\cdot3\cdot2\cdot1\cdot13!)=(1028160)/(120)=8568`

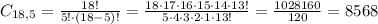
1 male:

`C_(10,1)=(10!)/(1!\cdot(10-1)!)=(10!)/(1\cdot9!)=(3628800)/(362880)=10`

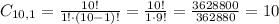
5 females and 1 male = 8568 * 10 = 85680

4th option:

6 females and 0 male:

`C_(18,6)=(18!)/(6!\cdot(18-6)!)=(18\cdot17\cdot16\cdot15\cdot14\cdot13\cdot12!)/(6\cdot5\cdot4\cdot3\cdot2\cdot1\cdot12!)=(13366080)/(720)=18564`
`C_(10,0)=(10!)/(0!\cdot(10-0)!)=(10!)/(10!)=1`

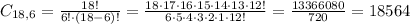
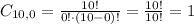
6 females and 0 male: 18564 * 1 = 18564

To finish the exercise, we have to sum the four options:

97920 + 137700 + 85680 + 18564 = 339864

So, right answer A: 339864.