Answer
The equation in point-slope form is
y - 1 = (-10/3) (x + 2)
We can then simplify this by multiplying through by 3 to obtain
3y - 3 = (-10) (x + 2)
3y - 3 = 10x - 20
3y = 10x - 20 + 3
3y = 10x - 17
Step-by-step explanation
The general form of the equation in point-slope form is
y - y₁ = m (x - x₁)
where
y = y-coordinate of a point on the line.
y₁ = This refers to the y-coordinate of a given point on the line
m = slope of the line.
x = x-coordinate of the point on the line whose y-coordinate is y.
x₁ = x-coordinate of the given point on the line
We can calculate the slope of the line and then use any of the two points given to serve as the point (x₁, y₁) in the equation
For a straight line, the slope of the line can be obtained when the coordinates of two points on the line are known. If the coordinates are (x₁, y₁) and (x₂, y₂), the slope is given as
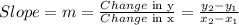
For this question,
(x₁, y₁) and (x₂, y₂) are (-5, 11) and (-2, 1)
x₁ = -5
y₁ = 11
x₂ = -2
y₂ = 1
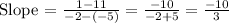
Slope = m = (-10/3)
Using the point (-2, 1) as (x₁, y₁), we can write the equation of the line
y - y₁ = m (x - x₁)
y - 1 = (-10/3) (x - (-2))
y - 1 = (-10/3) (x + 2)
We can then simplify this by multiplying through by 3 to obtain
3y - 3 = (-10) (x + 2)
3y - 3 = 10x - 20
3y = 10x - 20 + 3
3y = 10x - 17
Hope this Helps!!!