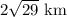Solution:
Given the points below
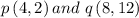
To find the distance between two points, the formula is
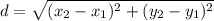
Where point p represents coordinates 1 and point q represents coordinates 2
Substitute the coordinates into the formula above
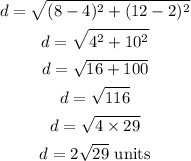
Since, 1 unit represents 1 kilometer on the map,
Hence, the answer is