1 Answer

Ask a Question

Prithajnath · Answer 1 · 2023-03-29T11:10:45+0000

From the problem, we are given a point (8, -6) and an equation y = 4x + 7

The equation we are to obtain is perpendicular to y = 4x + 7

In Mathematical terms, it means the slope of the given equation and the one we are to find follow the relation:

$\begin{gathered} m_1\text{ = }\frac{-1}{m_2_{}_{}} \\ \text{where m}_{1\text{ }}\text{represents the slope of the first equation and }m_2\text{ represents the slope of the second equation} \end{gathered}$

slope of the given equation = 4

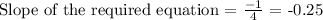
$\text{Slope of the required equation = }(-1)/(4)\text{ = -0.25}$

The required equation passes through a point (8,-6)

The formula for obtaining the equation with a given slope that passes through a point is given as :

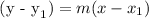
$\text{ (y - y}_1)=m(x-x_1)$

By substituting;

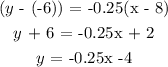
$\begin{gathered} (y\text{ - (-6)) = -0.25(x - 8)} \\ y\text{ + 6 = -0.25x + 2} \\ y\text{ = -0.25x -4} \end{gathered}$

The equation in slope-intercept form is y = -0.25x - 4

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions