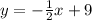Explanation.
The question asked us to write the equation of the line that passes through the points (2,8) and (-2,10)
To do this, we can use the formula:
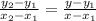
In our case, we have
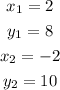
We will simply put all the values above into the formula to get the equation of the line
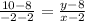
Simplifying further
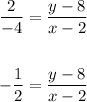
Cross multiplying
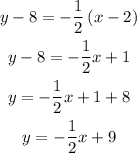
Therefore, the equation of the line is