Question

According to a study of the power quality (sags and swells) of a transformer, for transformers built for heavy industry, the distribution of the number of sags per work has a mean of 346 with a standard deviation of72. Of interest is x, the sample mean number of sags per week for a random sample of 216 transformers. Completo parts a through d below.a. Find E(%) and interpret its valueE() -(Type an integer or a decimal. Do not round.)Interpret the value of E(). Select the correct choice below and fill in the answer box to complete your choice(Type an integer or a decimal. Do not round.)O A. For any random sample of 216 transformers, the mean number of sags por wook is always. B. 1 many random samples of 216 transformers are taken, then the mean of the sample variances is sags por wookOC. If many random samples of 218 transformers are taken, then the mean of the sample mean numbers of sags per week isOD. I many random samples of 216 transformers are taken, then the mean of the sample standard deviations is sags por wookb. Find Var()Var) -(Type an integer or a decimal Round to three decimal places as needed.)c. Describe the shape of the sampling distribution of Xwith mean - and standard deviation -(Type intogors or decimal Round to three decimal places as needed)The sampling distribution of xd. Howey is it to observe a sample mean number of sags por wook that exceeds 3007C

Answer 1

Given data:

Population Mean = 346

Standard Deviation = 72

Expected Value of e(x) = population mean = 346

Sample Size = 216

In this case, if many random samples of 216 are taken, then the mean of the sample mean numbers per week is 346. (Option C)

To solve for the variance of x or var(x), we follow the formula below:

`var(x)=(\sigma^2)/(n)=\frac{(s\tan darddeviation)^2}{\text{sample size}}`

In this case, the given standard deviation is 72 and the sample size is 216. Therefore, we have:

`var(x)=(72^2)/(216)=(5184)/(216)=24`

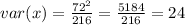
One of the properties of the Sampling Distribution of the Mean is that the sampling distribution of the mean is approximately normally distributed so long as the sample size is 30 or higher. Our sample mean here is 346 with a sample standard deviation of √24 or 4.899.

How likely is it to observe a sample mean number of sags per week that exceeds 390?

For this one, we have this formula to use:

`z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt[]{n}}}`

Our bar "x" is 390. The "myu" symbol is our population mean which is 346. This σ symbol is the population standard deviation 72 and n is our sample size = 216.

`z=\frac{390-346}{\frac{72}{\sqrt[]{216}}}=\frac{44}{2\sqrt[]{6}}=8.98`

Under a normal curve, the areas defined are between z = -3.5 to z = +3.5. Since our z should exceed > 8.98 and thus far greater than +3.5, then we can say that the probability of having a sample mean that exceeds 390 is zero.