Question

The two options I selected was incorrect, what would the answer be?

Answer 1

The question gives us the following function:

`f(x)=(3x)/(x-2)`

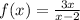
The X-intercept is where the function crosses the x-axis and the Y-intercept is where the function crosses the y-axis.

X-intercept:

Since the graph must cross the x-axis to have an x-intercept, we should equate f(x) to zero.

`\begin{gathered} f(x)=(3x)/(x-2)=0 \\ \\ 3x=0 \\ \therefore x=0\text{ is the x-intercept} \end{gathered}`

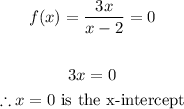
Y-intercept:

Since the graph must cross the y-axis to have a y-intercept, we should equate x = 0.

`\begin{gathered} f(x)=(3x)/(x-2) \\ \\ f(0)=(3(0))/(0-2) \\ \\ f(0)=0\text{ is a y-intercept} \end{gathered}`

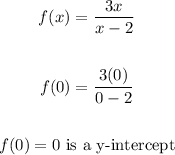
Answer

Thus, the x and y-intercepts are: x = 0 and y = 0 respectively