Question

How to subtract mixed fractions with different denominators

Answer 1

What you need to know:

product - the answer you get when multiplying

numerator - the top number in a fraction

denominator - the bottom number in a fraction

improper fraction - a fraction where the numerator is a bigger number than the denominator

So let's start off with an example:

2
`(1)/(4)` - 1
`(2)/(3)`

Because these are mixed fractions, we'll change them to improper fractions. We'll start with the first mixed fraction.

Step 1:

Multiply the whole number with the denominator of the fraction.

2
`(1)/(4)` In this case, we'll be multiplying 2 and 4, which is 8.

Step 2:

Add the product with the numerator.

8 + 1 = 9

Step 3:

Place the number 9 into the numerator, while still keeping the denominator the same:

`(9)/(4)`

Step 4:

Repeat steps one through three for the second mixed fraction.

Now you have this:

`(9)/(4)` -
`(5)/(3)`

Step 5:

Find the least common multiple of the two fractions.

(Let me know if you don't know how to do this).

Your result should be:

`(27)/(12) - (20)/(12)`

Step 6:

Subtract across, while still keeping the denominator the same:

`(27)/(12) - (20)/(12)` =
`(7)/(12)`

(Only do if needed) Step 7:

Simplify the fraction

Hope this helps, & if you have any questions, let me know!

Also, this is how I was taught to do it, and I'm not sure if there's a different way to solve it, but here's my work! :D

Answer 2

rewrite them with a common denominator

Explanation:

We assume your "mixed fraction" is an integer together with a fraction, such as 1 1/2.

There are at least a couple of ways to do this.

1. Perform the arithmetic separately on the integers and fractions, then combine results.

2. Convert both to improper fractions and do the subtraction. Then convert back to a mixed fraction.

__

Either way, fractions can only be added or subtracted if they have a common denominator. That can be achieved a couple of ways.

a) use the least common multiple (LCM) of the denominators as the common denominator. The LCM of the denominators is usually called the "least common denominator" (LCD). Example: 1/4 + 1/6 = 3/12 + 2/12 = 5/12

b) use the product of the denominators as the common denominator. Example: 1/4 +1/6 = 6/24 +4/24 = 10/24

Using the LCD tends to reduce the need for reducing the resulting fraction, because at least one common factor has already been removed. In the above examples, the fraction 10/24 still has factors of 2 that can be removed to reduce the fraction: 10/24 = (5·2)/(12·2) = 5/12

__

In general the difference of fractions can be found with a formula:

`(a)/(b)-(c)/(d)=(ad-bc)/(bd)`

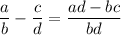
You will notice this has a denominator that is the product of denominators, so there is a good chance the result will have to be reduced to lowest terms. This can be quick and easy if you don't want to spend time trying to find the least common denominator.

_____

Here are a couple of examples:

(16 3/10) -(5 1/6) = (16 -5) +(3/10 -1/6) = 11 +(18 -10)/(10·6) = 11 8/60 = 11 2/15 (using methods 1 and b)

(16 3/10) -(5 1/6) = 163/10 -31/6 = 489/30 -155/30 = 334/30 = 167/15 = 11 2/15 (using methods 2 and a; note we had to reduce the final fraction even though we used the LCD)

In the above examples, there was no "borrow" due to the difference of the fractional parts. Here's an example where the difference of fractions affects the integer:

(16 1/6) -(5 3/10) = (16 -5) +(1/6 -3/10) = 11 +(10 -18)/60 = 11 -8/60

= 11 -2/15 = 10 13/15 (again, using methods 1 and b)

_____

Additional comments

You may have guessed that I prefer methods 1 and b, simply because they are quick and easy and tend to eliminate sources of error. As with all things arithmetic, it is very helpful to have a good command of multiplication tables, and a reasonable understanding of divisibility rules.

A suitable calculator can check your work for you. Mine makes mixed-number arithmetic very simple. Many graphing calculators have methods for entering and displaying mixed numbers. (I've found one that tries to express any decimal as a fraction, sometimes getting it very wrong. So, be careful if you have one of those.)