Since y is a parabolla, there will be two values for y = 19. We already know that x = 1 is one value, to find the other, we can substitute y = 19 on the equation and solve for x to get the following:
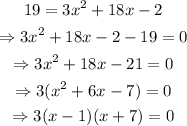
the solutions of the equation are x = 1 and x = -7. Since we already have that (1,19) is a point on the graph, then we have that the other point is (-7,19)