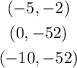Question

+ 16x + 71 tion provided to write the vertex form equation of each parabola 2) y = x² - 2x - 5 y=ola-h2xmin Ye21XR125 Identify the vertex and axis of symmetry of each. Then sketch the graph. 15) f(x)=-3(x - 2)2 - 4 16) S(x)=-1)+4 po

Answer 1

Vertex

General equation of a parable

`f(x)=a(x-h)^2+k`

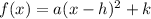
where

`(h,k)`

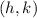
is the vertex

for our equation

`f(x)=-2(x+5)^2-2`

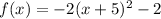
the vertex is

`(-5,-2)`

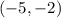
axis of symmetry

axis of symmetry is the x value of the vertex, then

`x=-5`

Graph

we replace values on x to find points of the parable

for example x=0

`\begin{gathered} f(0)=-2(0+5)^2-2 \\ f(0)=-2(5)^2-2 \\ f(0)=-2*25-2 \\ f(0)=-50-2 \\ f(0)=-52 \end{gathered}`

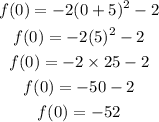
x=-10

`\begin{gathered} f(-10)=-2(-10+5)^2-2 \\ f(-10)=-2(-5)^2-2 \\ f(-10)=-2*25-2 \\ f(-10)=-50-2 \\ f(-10)=-52 \end{gathered}`

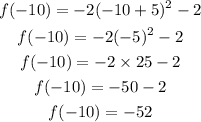
our three points

`\begin{gathered} (-5,-2) \\ (0,-52) \\ (-10,-52) \end{gathered}`