Answer
The probability that X > 90 is 84.13%
SOLUTION
Problem Statement
The question requires us to find the probability that X is greater than 90 if X is a variable from a normal distribution with a population mean (µ) of 100 and population standard deviation(σ) of 10.
Method
- The normal distribution gives the probability density curve that helps us predict the probability of a certain event happening. This probability is represented by the area under this normal distribution curve.
- The event in question here is when X > 90. We need to find the area under the curve where this inequality is true; this area under the curve will give us the probability that X > 90 as requested in the question. This area is depicted below:
- To find the area under the curve (or Probability), we need to:
1. Find the Z-score associated with the inequality X >90 given a normal distribution of population mean of 100 and population standard deviation of 10. We use the formula below to find the Z-score:
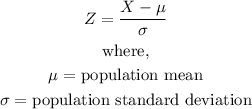
2. Convert the Z-score to a probability using a Z table or a Z-score calculator. This probability is the probability we are looking for
Implementation
1. Find the Z-score:
![\begin{gathered} X=90 \\ \mu=100 \\ \sigma=10 \\ \\ \therefore Z=(90-100)/(10)=-(10)/(10)=-1 \\ \\ \text{ Since we are asked to find }X>90,\text{ this implies that we should find the probability that corresponds to:} \\ Z>-1 \\ \\ \text{That is, we should find }P(Z>-1) \end{gathered}]()
2. Convert Z-score to probability:
Let us check the Z-distribution table to find the probability that corresponds to the Z-score.
In the Z-score table, we have:
This Z-score represents P(Z< -1) = 0.1587 (according to the table itself). But because we are looking for P(Z > -1), we need to subtract our answer from 1 to get the area under the curve to the right of X > 90.
That is:
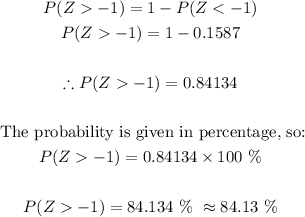
Final Answer
The probability that X > 90 is 84.13%