Question

A certain drug is eliminated from the bloodstream exponentially with a half-life of 12 hours. Suppose that apatient receives an initial dose of 25 milligrams of the drug at midnight. Estimate when the drugconcentration will reach 20% of its initial level. Round the answer to the nearest whole number.

Answer 1

Determine 20% of the initial level

20% → 0.2

`25\text{ mg}\cdot0.2=5\text{ mg}`

Write the equation with half-life of 12 hours and initial dose of 25 mg.

`y=25\cdot\Big((1)/(2)\Big)^{(t)/(12)}`

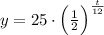
Substitute y = 5, and solve for t

`\begin{gathered} y=25\cdot\Big{(}(1)/(2)\Big{)}^{(t)/(12)} \\ 5=25\cdot\Big{(}(1)/(2)\Big{)}^{(t)/(12)} \\ (5)/(25)=\frac{\cancel{25}\cdot\Big{(}(1)/(2)\Big{)}^{(t)/(12)}}{\cancel{25}} \\ (1)/(5)=\Big{(}(1)/(2)\Big{)}^{(t)/(12)} \end{gathered}`

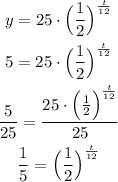
Get the natural logarithm of both sides

`\begin{gathered} \ln (1)/(5)=\ln \Big{(}(1)/(2)\Big{)}^{(t)/(12)} \\ \ln (1)/(5)=(t)/(12)\cdot\ln \Big{(}(1)/(2)\Big{)}^{} \\ t=(12\ln (1)/(5))/(\ln (1)/(2)) \\ t=27.86313714 \end{gathered}`

Rounding the answer to the nearest whole number, the time it takes for the initial dose to be reach 20% of its initial level is 28 hours.