Question

Determine how many solutions does this equation system have.y=-3x+4y=4x-10help me

Answer 1

Given the equations

`y=-3x+4`
`y=4x-10`

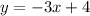
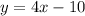
Since both equations are written for y, you can equal them

`\begin{gathered} y=y \\ -3x+4=4x-10 \end{gathered}`

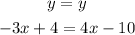
From this expression, you can determine the value of x, the first step is to pass all x-like terms to the left side of the equal sign and the constants to the right side. To pass the terms from one side to the other you have to apply the opposite operation to the whole expression.

This means that if 4 is "adding" on the left side, to pass it to the right side, you have to subtract "4" from both sides

`\begin{gathered} -3x+4-4=4x-10-4 \\ -3x=4x-14 \end{gathered}`

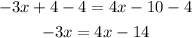
Repeat the procedure to pass "4x" to the left side

`\begin{gathered} -3x-4x=4x-4x-14 \\ -7x=-14 \end{gathered}`

Now to determine the value of x, divide both sides of the equation by -7

`\begin{gathered} (-7x)/(-7)=(-14)/(-7) \\ x=2 \end{gathered}`

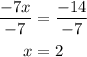
Now that the value of x is calculated, replace it in either one of the original equations to determine the corresponding value of y

`\begin{gathered} y=-3x+4 \\ y=-3\cdot2+4 \\ y=-2 \end{gathered}`

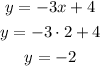
This equation system has one solution at points (2,-2)