in Example #2,
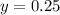 or
or
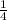 when rounded to the nearest hundredth.
when rounded to the nearest hundredth.
in Example #1,
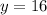 .
.
Here are the detailed steps to solve the proportions for
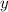 :
:
Example #1:
The proportion is given by:
![\[ (4)/(9) = (y)/(36) \]](https://img.qammunity.org/2023/formulas/mathematics/college/kcyhjdfldzcgy0p1mr9rlzah5pu2dvlndg.png)
To solve for
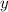 , cross-multiply to get:
, cross-multiply to get:
![\[ 4 * 36 = 9 * y \]](https://img.qammunity.org/2023/formulas/mathematics/college/b2wptj91h8poeo91iiq05w67t0m29wcpmw.png)
![\[ 144 = 9y \]](https://img.qammunity.org/2023/formulas/mathematics/college/h6j6ynn6g49v95pmi5lbc7q2pybwi07tmh.png)
Now, divide both sides by 9 to isolate
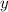 :
:
![\[ y = (144)/(9) \]](https://img.qammunity.org/2023/formulas/mathematics/college/ktnrbam8wq6p1nhtk5cknewfdzpv0ex7yn.png)
![\[ y = 16 \]](https://img.qammunity.org/2023/formulas/mathematics/college/lz2w63z3fhnm5sn9n8genpkdojjfnuwuls.png)
So, in Example #1,
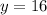 .
.
**Example #2:**
The proportion is given by:
![\[ (72)/(1.5) = (12)/(y) \]](https://img.qammunity.org/2023/formulas/mathematics/college/vdjjygtas2ilt003sha4ftfrroy76cemhz.png)
To solve for
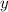 , cross-multiply to get:
, cross-multiply to get:
![\[ 72 * y = 12 * 1.5 \]](https://img.qammunity.org/2023/formulas/mathematics/college/k6n21egfy76eb478alek9ggmlb075cgmcf.png)
![\[ 72y = 18 \]](https://img.qammunity.org/2023/formulas/mathematics/college/dv1o1zlllrtt47vrsgivg5wk1nv5o450u7.png)
Now, divide both sides by 72 to isolate
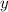 :
:
![\[ y = (18)/(72) \]](https://img.qammunity.org/2023/formulas/mathematics/college/vu92z8o22t3qhjffm9qlnobp49e1llp2yn.png)
![\[ y = 0.25 \]](https://img.qammunity.org/2023/formulas/mathematics/college/fvxz86ztzxc5qkmqezd4xns4pjpprvwjh6.png)
So, in Example #2,
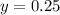 or
or
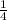 when rounded to the nearest hundredth.
when rounded to the nearest hundredth.